ABSTRACT
Conventionally broadcast encryption (BE) schemes enable a sender to securely broadcast to any subset of members, however it requires a trusted party to circulate decryption keys. Group key agreement protocols authorize a group of members to negotiate a common encryption passkey through spread out networks so that only the batch members can decode the ciphertextsviz encrypted under the shared encryption key, but a sender cannot debar any particular member from decrypting the ciphertexts. This project infers two notions with a hybrid primitive referred to as Auxiliary Propagate encoding. In this new primitive, a common public encoding key is agreed by group members who hold a individual decoding passkey. A sender viewing the public group encoding passkey can restrict the decoding to a subdivision of members of his preference. The scheme is proven to be fully collusion-resistant under the decision n-Bilinear Diffie-Hellman Exponentiation presumption in the standard imitation. Of unaided interest, the project presents a new BE scheme that is aggregatable. The cumulative property is shown to be useful to construct advanced protocols.
Keywords-Multicast encoding, Auxiliary Propagate Encoding, Provable Security, Group key agreement
INTRODUCTION
- INTRODUCTION
Along the rapidly leading and prevalent communion technologies, there is an increasing bid for handy cryptographic primeval to protect group conversations and ciphering platforms. These platforms include instant-messaging tools, collaborative ciphering, mobile ad hoc networks and communal net. These new applications call for cryptographic primitives allowing a sender to soundly encrypt to any subdivision of the users of the services without relying on a fully credible dealer. Broadcast encoding is a well-studied primeval intended for secure group-oriented communications. It allows a sender to soundly broadcast to any subdivision of the group members
Nonetheless, a BE system heavily relies on a fully trusted key server who produces classified decoding passkeys for the members and can read all the communion to any members. Group key agreement is another well-defined cryptographic primeval to secure group-oriented communions. A traditional GKA enables a group of members to setup a common secret passkey through spread out networks. However, whenever a sender wants to share an information to a group, he must first join the group and run a GKA protocol to share a classified passkey with the intended members. More recently, and to overthrow this limitation, Wu et al. popularized asymmetric GKA, a common public encoding key is agreed by group members who hold a individual decoding passkey. However, neither traditional symmetric GKA nor the newly introduced asymmetric GKA enables the sender to unilaterally exclude any particular member from reading the plaintext. Hence, it is necessary to find several adjustable cryptographic primeval enabling dynamic broadcasts without a fully credible dealer.
Get Help With Your Essay
If you need assistance with writing your essay, our professional essay writing service is here to help!
The Auxiliary Propagate Encoding primitive, viz a hybrid of GKA and BE. Compared to its preliminary Asia crypt 2011 version, this project provides complete security proofs, elaborates the necessity of the aggregatability of the hidden BE building block and shows the practicality of the scheme with experiments. The main contributions are as follows. First, the primitive and explains its security definitions. Auxiliary Broadcast Encoding incorporates the elemental ideas of GKA and BE. A group of members interact through free networks to agree a public encoding passkey while each member holds a different secret decoding key. Using the public encryption passkey, anyone can encode any message to any subdivision of the group members and only the intended receivers can decrypt.
Unlike GKA, Auxiliary enables the sender to exclude some members from reading the ciphertexts. Compared to Broadcast Encryption, Auxiliary Propagate Encoding does not need a fully credible third party to set up the system. Characterize collusion resistance by defining an attacker who can fully control every member farther the affianced receivers but cannot extract useful message from the cipher text.
Second, the notion of aggregatable broadcast encoding. Coarsely speaking, a Broadcast Encoding scheme is aggregatable if its secure instances can be aggregated into a new secure instance of the BE system. Specifically, only the aggregated decoding keys of the same user are valid decoding keys corresponding to the aggregated public passkeys of the hidden Broadcast Encryption examples. The aggregatability of AggBE schemes is beneficial in the manufacturing of scheme and the BE schemes in the literature are not aggregatable. A detailed AggBE system tightly proven to be fully collusion-resistant beneath the decision BDHE assumption. The proposed AggBE system offers effectual encoding/decoding and short ciphertexts.
Certainly, create an effectual Auxiliary Broadcast Encoding scheme with AggBE scheme as a building block. The Auxiliary Broadcast Encoding construction is proven to be semi-adaptively secure under the decision Bilinear Diffie-Hellman Exponentiation assumption in the standard model. Only one round is needed to form the public group encoding passkey and set up the Auxiliary Broadcast Encoding system. After the system set-up, the storage cost would be O(n) for sender as well as for group members, where n is the number of group members taking part in the setup stage. Although, the online complexity (which dominates the practicality of a Auxiliary Broadcast Encoding scheme) is very low. Post trade-off, the variant has O(n2=3) complexity in communion, calculations and storage. This is comparable to up-to-date regular Broadcast Encoding schemes which have O(n1=2) complexity in the same performance metrics, but system does not require a credile passkey dealer. Execute a chain of experiments and the experimental results verify the practicality of scheme.
Potential Applications
A potential application of Auxiliary Propagate Encoding is to secure data exchanged among friends via social networks. Since the Prism scandal, people are desperately concerned about the privacy of their personal data shared with their friends over social networks. Auxiliary Propagate Encoding can provide a feasible solution to this problem. Indeed, Phan et al underlined the applications of Auxiliary Propagate Encoding to social networks. In this scenario, if a group of users want to share their data without letting the social network operator know it, they this Encoding scheme. Since the setup procedure of Encoding only requires one round of communication, each member of the group just needs to broadcast one message to other intended members in a send-and-leave way, without the synchronization requirement. After receiving the messages from the other members, all the members share the encryption key that allows any user to selectively share his/her data to any subgroup of the members. Furthermore, it also allows sensitive data to be shared among different groups. Other applications may include contemporary messaging among family members, protected scientific research tasks jointly conducted by scientists from different places, and disaster rescue using a mobile ad hoc network. A common feature of these scenarios is that a group of users would like to exchange sensitive data but a fully credible third party is unavailable. Encoder provides an efficient solution to these applications.
AIMS & OBJECTIVES
2.1 AIM
The Auxiliary Propagate Encoding primitive, viz a hybrid of GKA and BE. Compared to its preliminary Asia crypt 2011 version, this project provides complete security proofs, elaborates the necessity of the aggregatability of the hidden BE building block and shows the practicality of the scheme with experiments. The main aim are as follows. First, the primitive and explains its security definitions. Auxiliary Broadcast Encoding incorporates the elemental ideas of GKA and BE. A group of members interact through free networks to agree a public encoding passkey while each member holds a different secret decoding key. Using the public encryption passkey, anyone can encode any message to any subdivision of the group members and only the intended receivers can decrypt.
Unlike GKA, Auxiliary enables the sender to exclude some members from reading the ciphertexts. Compared to Broadcast Encryption, Auxiliary Propagate Encoding does not need a fully credible third party to set up the system. Characterize collusion resistance by defining an attacker who can fully control every member farther the affianced receivers but cannot extract useful message from the cipher text.
2.2 OBJECTIVE
- The Auxiliary propagate Encoding primitive, which is a hybrid of GKA and BE.It provides complete security proofs, illustrates the necessity of the aggregatability of the underlying BE building block.
- ConBE incorporates the underlying ideas of GKA and BE. A group of members interact via open networks to negotiate a public encryption key while each member holds a different secret decryption key. Using the public encryption key, anyone can encrypt any message to any subset of the group members and only the intended receivers can decrypt.
- The collusion resistance by defining an attacker who can fully control all the members outside the intended receivers but cannot extract useful information from the ciphertext.
- The notion of aggregatable broadcast encryption (AggBE). Coarsely speaking, a BE scheme is aggregatable if its secure instances can be aggregated into a new secure instance of the BE scheme.
- Specifically, only the aggregated decryption keys of the same user are valid decryption keys corresponding to the aggregated public keys of the underlying BE instances.
- An efficient ConBE scheme with our AggBE scheme as a building block. The ConBE construction is proven to be semi-adaptively secure under the decision BDHE assumption in the standard model.
LITERATURE
SURVEY
- LITERATURE SURVEY
3.1 Paper on Broadcast Encryption: Several schemes that allow a center to broadcast a secret to any subset of privileged users out of a universe of size nso that coalitions of k users not in the privileged set cannot learn the secret. The most interesting scheme requires every user to store O(k log k Several schemes that allow a center to broadcast a secret to log n)keys and the center to broadcast O(k2 log2 k log n) messages regardless of the size of the privileged set. This scheme requires every user to store O(log k log(1/p)) keys and the center to broadcast O(k log2 k log(1/p)) messages.
Algorithm:
Step 1: Takes as input the number of receivers n, Setup(n) outputs private keys d1 , …, dn and public-key PK.
Step 2: Takes as input a subset, Encrypt (S, PK, M): Encrypt M for users S ïƒ {1, …, n} Output ciphertext CT.
Step 3: Takes as input a subset, Decrypt (CT, S, j, dj, PK): If j  S, output M.
The key K can then be used to decrypt the broadcast body CM and obtain the message body M
3.2 Paper on Collusion Resistant Broadcast Encryption With Short Ciphertexts and Private Keys: This system describe two new public key broadcast encryption systems for stateless receivers. Both systems are fully secure against any number of colluders. This construction both ciphertexts and private keys are of constant size (only two group elements), for any subset of receivers. The public key size in this system is linear in the total number of receivers. Second system is a generalization of the first that provides a trade-off between ciphertext size and public key size. The system achieves a collusion resistant broadcast system for n users where both ciphertexts and public passkeys are of size O(√n) for any subset of receivers.
Algorithm:
Step 1: Let G be a bilinear group of order p. Pick a random generator g of G and random α, γ ∈ Zp and, as usual, define gi = g(α i ) and v = gγ∈ G.
Step 2: Output the public key PK = {g, g1, … , gn, gn+2, . . . , g2n, v} , it generates m shares of γ. Secret sharing generates the shares. Let f ∈ Zp[x] be a random polynomial of degree t − 1 satisfying f(0) = γ. For j = 1, … , m the j’th share of γ is defined as sj = f(j) ∈ Zp.
Step 3: User k ∈ {1, . . . , n} wants her private key dk = g γk∈ G. pick t administrator servers to help generate dk. To generate dk . For i = 1, . . . , it receives g si k from the ith administrator. It computes private key as dk = âˆi=1(gk8)λi . Then dk = gk∑i=1 λi8i = g γk as required. As usual all these messages are sent between the administrators and a user are over a private channel.
3.3 Paper on A Conference Key Distribution System: Encryption is used in a communication system to safeguard information in the transmitted messages from anyone other than the intended receiver. To perform the encryption and decryption the transmitter and receiver ought to have matching encryption and decryption keys. A clever way to generate these keys is to use the public key distribution system invented by Diffie and Hellman.
The public key distribution system is generalized to a conference key distribution system (CKDS) which admits any group of stations to share the same encryption and decryption keys. The analysis reveals two important aspects of any conference key distribution system.
One is the multi-tap resistance, which is a measure of the information security in the communication system. The other is the separation of the problem into two parts: the choice of a suitable symmetric function of the private keys and the choice of a suitable one-way mapping thereof.
Algorithm :
Step 1 : Consider A center chooses a prime p = Θ(2cN), c ≥ 1 constant, and an element α ∈ Zp of order q = Θ(2N). If this has to be veriï¬ed then the factorization of q is given. The center publishes p, α and q.
Step 2 : Let U1,…,Un be a (dynamic) subset of all users5 who want to generate a common conference key.
Step 3 : Each Ui, i = 1,…,n, selects6 ri∈R Zq, computes and broadcasts Zi=αri mod p .
Step 4 : Each Ui, i = 1,…,n, checks7 that αq ≡ 1(modp) and that (zj)q ≡ 1(modp) for all j = 1,…,n, and then computes and broadcasts
Xi ≡(zi+1/zi−1)ri (modp),
where the indices are taken in a cycle.
Step 5 : Each Ui, i = 1,…,n, computes the conference key,
Ki ≡(zi−1)nri ·Xin-1−1 · Xi+1n-2 ··· Xi-2 (modp).
3.4 Paper on Key Agreement in Dynamic Peer Groups:
As a result of the increased popularity of group- oriented applications and protocols, group communication occurs in many different settings: from network multicasting to application layer tele- and video-conferencing. Regardless of the application environment, security services are necessary to provide communication privacy and integrity. This paper considers the problem of key agreement in dynamic peer groups. (Key agreement, especially in a group
setting, is the steeping stone for all other security services.)Dynamic peer groups require not only initial key agreement (IKA) but also auxiliary key agreement (AKA) operations
such as member addition, member deletion and group fusion. We discuss all group key agreement operations and present a concrete protocol suite, CLIQUES, which offers
complete key agreement services. CLIQUES is based on multi-party extensions of the well-known Diffie-Hellman key exchange method. The protocols are efficient and provably
secure against passive adversaries.
3.5 Comparative Study
|
SR NO |
Paper Title And Methods Used |
Author’s Name |
Mertis |
Demerits |
Problem |
Solution |
Future Work |
|
1. |
Broadcast Encryption ( Symmetric Encryptions, Secret key Distributions & management) |
A. Fiat and M. Naor |
Provides secure group-oriented communications |
Existing GKA protocols cannot handle sender/member changes efficiently |
Requires a trusted third party to distribute the keys. |
Using Asymmetric group key agreement (ASGKA) to overcome this. |
Future work will concern the implementation of the ASGKA scheme to incorporate the following. |
|
2. |
Collusion Resistant Broadcast Encryption with short Ciphertext and private keys (Parameterization) |
Dan Boneh , Craig Gentry |
Provides a collusion resistant system. |
Cannot handle large sets of groups. |
Collusion resistant is limited to a relatively small group. |
Using appropriate parametrization |
Future works will concern the reduction of collusion by constructing both Ciphertext and private key of constant size. |
|
3. |
A Conference Key Distribution System (Security in digital systems ,Conference key distribution) |
I. Ingemarsson, D.T. Tang and C.K. Wong |
Provides a system using That distributes key using contributory key generation. |
It is immune to insecurities due to symmetric functions of degree two. |
As the key was a symmetric function of degree two, it was insecure. |
Using a asymmetric function instead of symmetric function. |
Future research will be devoted to methods that can use asymmetric function for higher security. |
|
4. |
Key Agreement in Dynamic Peer Groups (Multi-party Computation) |
Michael Steiner, |
Can handle system with constantly changing members and senders. |
It is not efficient for relatedly large set of groups. |
Works only for relatively small and non-hierarchical groups. |
Using key transport mechanism. |
Future research Will including the methods adopted in this. |
|
5. |
Broadcast Encryption ( Symmetric Encryptions, Secret key Distributions & management) |
A. Fiat and M. Naor |
Provides secure group-oriented communications |
It requires a fully trusted third party and direct link |
It is more expensive as direct link has to be established |
Cost can be minimised using Contributory key generation schemes or using Conbe Scheme. |
Future research will be including plans to implement the schemes to cut down expenses. |
|
6. |
Contributory Broadcast Encryption With Efficient Encryption and Short Ciphertexts |
Qianhong ,Bo Qin, Lei Zhang,Josep Domingo-Ferrer |
Doesn’t require trusted third Party to set up the system. |
As it is more flexible , it compromises on some set of performances. |
Cannot handle changes in server/member efficiently |
Using auxiliary group Encoding |
EXISTING SYSTEM
- EXISTING SYSTEM
PROBLEM STATEMENT
- PROBLEM STATEMENT
The prevailing broadcast encryption scheme can provide reliable end to end encryption, however requires a trusted third party to distribute the keys. Also the BE scheme requires to set a direct link with the receiver to enable the flow of information. Existing GKA protocols cannot handle sender/member the changes efficiently with the growing technologies and ad hoc devices, it is essential for the system to address and resolve the issue.Using Asymmetric group key agreement (ASGKA) the system can overcome the shortcomings of the BE system.
Collusion Resistant Broadcast Encryption with short Ciphertext and private keys methodology used a symmetric key of degree two to mitigate collusion for a relatively short system. It could not handle or further avoid collusion for a large set of system.Using appropriate parameterization can aid the drawbacks of the system. Also as the key was a symmetric function of degree two, it was insecure and worked only for relatively small and non-hierarchical groups.
Find Out How UKEssays.com Can Help You!
Our academic experts are ready and waiting to assist with any writing project you may have. From simple essay plans, through to full dissertations, you can guarantee we have a service perfectly matched to your needs.
View our academic writing services
A Conference Key Distribution System which uses security in digital systems and conference key distribution provides a system That distributes key using contributory key generation. It is immune to insecurities as it uses symmetric function of degree two. Key Agreement in Dynamic Peer Groups which uses multi-party Computation can handle system with constantly changing members and senders but It is not efficient for relatedly large set of groups. Using key transport mechanism, the range of the system can work efficiently for relatively larger set of group. The system will not require the sender to be the part of the group.
SCOPE
- SCOPE
PROPOSED SYSTEM
- PROPOSED SYSTEM
- Diffie-hellman algorithm
Diffie-Hellman key exchange (D-H) [nb 1] is a specific method of securely exchanging cryptographic keys over a public channel and was one of the first public-key protocols as originally conceptualized by Ralph Merkle and named after WhitfieldDiffie and Martin Hellman.
Step 1: Let the users be named sender and receiver. First, they agree on two prime numbers g and p, where p is large and g is a primitive root modulo p.
Step 2: Now sender chooses a large random number a as her private key and receiver similarly chooses a large number b.
Step 3: Sender then computes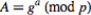 , which she sends to Receiver, and Receiver computes
, which she sends to Receiver, and Receiver computes 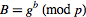 , which he sends to sender.
, which he sends to sender.
Step 4: Now both Sender and Receiver compute their shared key 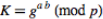 , which Sender computes as
, which Sender computes as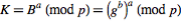 and Receiver computes as
and Receiver computes as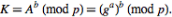
Sender and Receiver can now use their shared key 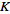 to exchange information without worrying about other users obtaining this information. In order for an attacker to do so, he would first need to obtain
to exchange information without worrying about other users obtaining this information. In order for an attacker to do so, he would first need to obtain 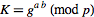 knowing only
knowing only  ,
, 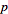 ,
, 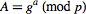 and
and 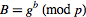 .
.
This can be done by computing  from
from 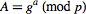 and
and 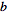 from
from 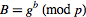 . This is the discrete logarithm problem, which is computationally infeasible for large
. This is the discrete logarithm problem, which is computationally infeasible for large 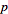 . Computing the discrete logarithm of a number modulo
. Computing the discrete logarithm of a number modulo 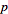 takes roughly the same amount of time as factoring the product of two primes the same size as
takes roughly the same amount of time as factoring the product of two primes the same size as 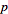 .
.
7.2MATHEMATICAL MODEL
Group Key Agreement. For 1 ≤k ≤n, member k doesthe following:
– Randomly choose Xi,k ϵG, ri,k ϵZp̽;
– Compute Ri,k = g־ʳi,k, Ai,k = e(Xi,k, g);
– Set PKk = ((R0,k , A0,k),….,(Rn,k, An,k));
– For j = 1,……., n ,j≠k, computeσi, j ,k=Xi,khjri,kfor i = 0,……,n, with i ≠j;
– Set dj,k = (σ0,j,k,….., σjÖ¾1,j,k,σj+1,j,k,……,σn,j;k);
– Publish (PKk, d1,k,…….,dkÖ¾1;k, dk+1,k,……., dn,k);
– Compute dk,k accordingly and keep it secret.
- Group Encryption Key Derivation. The group encryption key is
PK = PK0 PKn = ((R0,A0),…………,(Rn,An))
where Ri =Пnk=1Ri,k,Ai =Пnk=1Ai,kfor i =0,………,n.
The group encryption key PK is publiclycomputable.
- Member Decryption Key Derivation: For 1 ≤i≤ n
1 ≤j≤ nand i ≠j, member j can compute herdecryption key
dj = (σ 0,j,….., σ j־1,j,σj+1,j,……,σn,j)
where
n n n
σi,j= σi,j,jПσi,j,k= Пσi,j,k= ПXi,khrj
k=1,k≠1 k=1 k=1
7.3 SYSTEM ARCHITECTURE
 Storage Server
Storage Server



 Upload File with privileges
Upload File with privileges




1. Req File & Search Files
2.Access the file

METHODOLOGY
- METHODOLOGY
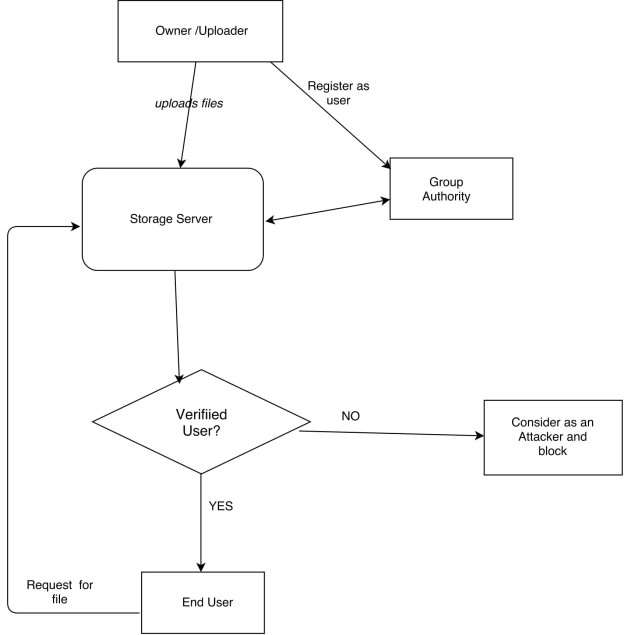
 8.1 FLOW CHART
8.1 FLOW CHART
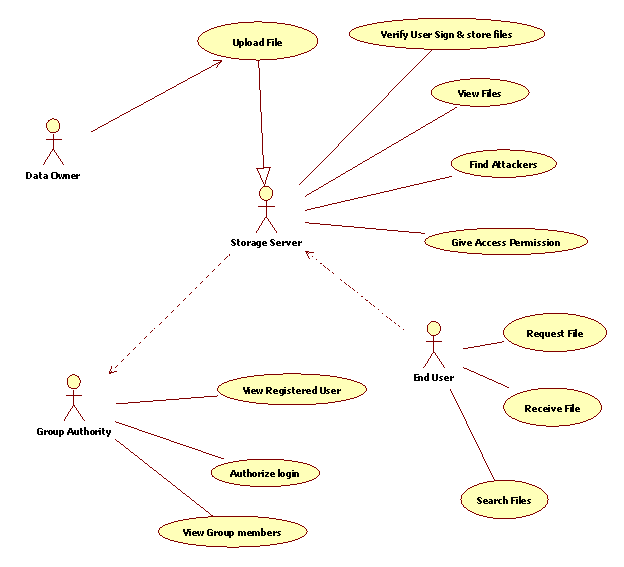
- UML DIAGRAMS
8.2.1 Use Case Diagram
- Sequence Diagram




 Upload Files
Upload Files
 Upload File Response
Upload File Response
 Register
Register
 Register Confirmation
Register Confirmation
 Provide access Permission
Provide access Permission
 Request & Search the file
Request & Search the file
 File request confirmation
File request confirmation

 File sending response
File sending response



 Req Sign Distribution
Req Sign Distribution


 Sign Res Status
Sign Res Status
- Class Diagram

Cite This Work
To export a reference to this article please select a referencing style below:
Give Yourself The Academic Edge Today
- On-time delivery or your money back
- A fully qualified writer in your subject
- In-depth proofreading by our Quality Control Team
- 100% confidentiality, the work is never re-sold or published
- Standard 7-day amendment period
- A paper written to the standard ordered
- A detailed plagiarism report
- A comprehensive quality report
Essay Writing Service
Essay Writing
Service
AED558.00
Approximate costs for Undergraduate 2:2
1000 words
7 day delivery
Order An Essay TodayDelivered on-time or your money back

1858 reviews

